月別アーカイブ: 2012年5月

ある会社に頼んでタンスの耐震対策をしてもらいました。そのビホォー、アフターです。従来取り付けていた“突っ張り棒”は余り効果がないそうで、それでもタンスの出来るだけ隅の２ヶ所がよりベターだそうです。今度のは、家具倒防止ストップベルト“役に立つぞ〜君”です。タンスをどかして畳を上げて床に穴を開けてベルトを通す、結構本格的なものです。写真のタンスの上を見て下さい、ベルトが見えます。また、下には、“踏ん張る君”を設置。昨年の地震の時には、これだけでも結構大丈夫だったそうです。ベルトの方は震度７強でもタンスが少し斜めに傾く程度だそうです。そして、私の大好きな様々なバカラの入ったガラス棚２つは、とりあえずやりようがないそうですが、下にゴムが付いているのでさほど心配は無いそうです。これは今後の課題になりました。ジョリーは私が施工あとを見ていると“何だ、何だ”と例によってついてきます。とりあえず、一安心です。東京都 算数、数学の個別指導塾、序理伊塾。

問題…Ａ＝ｓｉｎ１゜、Ｂ＝ｔａｎ１゜、Ｃ＝１−ｃｏｓ２゜ の大小関係を答えなさい。解答と解説…Ｂ／Ａ ＝ｓｉｎ１゜／ｓｉｎ１゜ｃｏｓ１゜ ＝１／ｃｏｓ１゜ ＞１ また、Ｃ＝１−(１−２ｓｉｎ１゜×ｓｉｎ１゜)＝２ｓｉｎ１゜×ｓｉｎ１゜ より、Ｃ／Ａ ＝２ｓｉｎ１゜＜２ｓｉｎ３０゜＝１ よって、Ｂ＞Ａ＞Ｃ…答えです。数学の普通の角度とラジアンの混ざった三角関数の問題です。見慣れ無い数学の問題ですが、慣れておいて下さい。個別指導塾の私の教室でも不慣れな生徒さんが多いようです。 東京都 算数、数学の個別指導塾、序理伊塾。

例によって朝の８時に自宅を出発、親水公園経由で錦糸公園へ。錦糸公園には既にマフちゃんとブランカちゃんがいました。噴水の縁に三人でノンビリ、マッタリ。近景にスカイツリーが見えます。東京都 算数、数学の個別指導塾、序理伊塾。

問題…２次方程式 ２ｘｘ−４ｘ−１＝０ の２つの解をａ、ｂとするとき(ａ＞ｂ)、ａａ＋ｂｂ−２ａ−２ｂ の値を求めなさい。解説と解答…解と係数の関係より、ａ＋ｂ＝２…ア ａｂ＝−１／２ …イ ａａ＋ｂｂ−２ａ−２ｂ＝(ａ＋ｂ)(ａ＋ｂ)−２ａｂ−２(ａ＋ｂ) は、ア、イ を代入して４＋１−４＝１…答えです。高校入試の数学でも解と係数の関係は大切です。大学入試の数学では勿論ですが。数学の個別指導塾として、私の教室では極力解と係数の関係を使うように薦めています。 東京都　算数　数学の個別指導塾、序理伊塾。

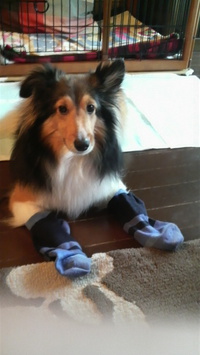
私が机に向かって本を読んだりしていると、ジョリーは必ず側に来てお座りをします。これは“ジョリーと遊んでちょうだい♪” のシグナルなのです。これを無視して本を読み続けるとジャンプをして本を叩き落とそうとします。そこで、私は本を中断して、ジョリーのお相手。先ずは、ユキちゃんをジョリーのオツムに。次は“ライトとレフト”、ジョリーはほぼ完璧にクリア。そこで私はジョリーに“くるぶしソックス”を履かせてみました。初めての試みです。ジョリーはちゃんと履いて伏せまでしました。すっかりお利口さんになったジョリーです。最後の遊びは写真にはありませんが、“引っ張り棒”で身体を使う遊び…。 ジョリーより私の方が疲れて今日のお遊び終了、あ〜疲れた。 東京都 算数、数学の個別指導塾、序理伊塾。

２１３４を３けたの数□で割ると、商と余りが等しくなります。□に当てはまる整数を求めなさい。解説と解答…２１３４を□で割った商と余りがともにＡであったとすると、２１３４＝□×Ａ＋Ａ＝Ａ×(□＋１) ここで、□は３桁の数なので、(□＋１) は １０１以上１０００以下の２１３４の約数です。２１３４を素因数分解すると、２×１１×９７ となるので、２×９７＝１９４ だけです。よって、□＝１９４−１＝１９３…答えです。算数でも分配法則は必須です。中身は簡単ですが手こずる人もいるかも知れません。算数の基本的な問題です。 東京都 算数、数学の個別指導塾、序理伊塾。

ジョリーを美容院にお預けして“巴潟”さんで食事をしてから、２、３軒隣にあるハイジのお店に行きました。ここには時折お邪魔します。明るい楽しいお店です。なかなか気が付かない場所にあるのですが、一度寄ってからは楽しいグッズを見たり買ったりしています。 東京都 算数、数学の個別指導塾、序理伊塾。

問題…ｘｘｘ−７ｘ＋９ が素数となるような整数ｘを求めなさい。解説と解答…ｘｘｘ−７ｘ＋９＝ｘｘｘ−ｘ−６ｘ＋９＝(ｘ−１)ｘ(ｘ＋１)−３(２ｘ−３) …ア ここで、(ｘ−１)ｘ(ｘ＋１) は、連続する３つの整数の積なので、３の倍数です。よって、アは３の倍数です。よって、これが素数になるときは！３のみです。ｘｘｘ−７ｘ＋９＝３ より ｘｘｘ−７ｘ＋６＝０ これより、(ｘ−１)(ｘ−２)(ｘ＋３)＝０ よって、ｘ＝１、２、−３…答えです。この数学の問題もよくあるパターンです。数学の個別指導塾の私の教室でも苦手な生徒さんが多いようです。素数は中学入試の算数にも頻繁に登場します。 東京都 算数数学の個別指導塾、序理伊塾。

今日はジョリーのシャンプーの日です。お世話になるのは、いつもの両国ドッグガーデン。朝の２時間散歩の後一休みして１１時に自宅を出発。先ずは教室の前でパチリ♪ そして美容院に到着してパチリ♪ ジョリーをお預けして私達は“巴潟”さんで遅い朝食兼昼食。何故か今日は個室に案内されました。食事が終わってアルプスの少女ハイジのお店で買い物。我が家にはまたまた幼稚なグッズが増えます。街をブラブラしているとシャンプー完了の電話。ジョリーを直ぐに迎えに行きます。ジョリーはママを見上げてとても嬉しそうです。そして仲良く三人で帰宅しました。 東京都 算数、数学の個別指導塾、序理伊塾。

問題…次の正方行列Ａ、Ｂについて、Ａ＋Ｂ＝ＡＢならば Ａ−Ｅ は逆行列を持つことを示しなさい。解説と解答…Ａ＋Ｂ＝ＡＢ から ＡＢ−Ａ−Ｂ＋Ｅ＝Ｅ よって (Ａ−Ｅ)(Ｂ−Ｅ)＝Ｅ したがって、Ａ−Ｅ は 逆行列 Ｂ−Ｅ を持つ。数学 Ｃ の行列の問題です。行列の問題は苦手な生徒さんが意外と多く、個別だとよくわかると喜んでもらっています。数学の苦手な生徒はそうなのかも知れません。 東京都 算数、数学の個別指導塾、序理伊塾。