<問題> 2直線 y = 3 x…➀、y = ー2 x+4…➁ においてこの2直線のなす角θを求めなさい。 <解説と解答> 求める角θは、原点を通る2直線 y = 3 x…➀ とy = ー2 x…➁′ のつくる角に等しい。➀、➁′ が x軸の正の向きとつくる角をそれぞれ α、β とすると、tanα=3、tanβ=ー2 となり、θ=βーα となるから、tanθ=tan(βーα)=(tanβーtanα)/(1+tanβ・tanα) =(ー2・3)/{1+(ー2)・3} =1 、0°≦ θ <180° の範囲で θを求めると、θ= 45°…答えです。簡単な問題ですが、大学入試の数学の課題です。y = ー2 x+4 を y = ー2 x に置き換えるのがポイントです。あとは、tanの加法定理です。➀と➁′ のグラフを書くと更によくわかると思います。序理伊塾では算数や数学を分かり易く教えることに努めています。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
月別アーカイブ: 2022年9月
ペットのお店、” コジマ さん”。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
2022年9月29日 先生と生徒(卒業生も)のふれあい広場








塾の近くのペットのお店の” コジマ さん”、久しぶりに行ってみました。ジョリーの散歩の際のおやつと塾から自宅に帰る時のお土産が無くなりそうだからです。お店は入り口が二つあります。右側かワンちゃん、ネコちゃん達がいる所になります。今日は丁度お昼寝タイムでガッカシ。でも、目的のものは全部、たっぷりと買えて満足。ジョリーもきっと喜んでくれることでしょう。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
大学入試の数学の問題です。算数個別、数学個別、序理伊塾。
2022年9月28日 先生と生徒(卒業生も)のふれあい広場
<問題> 直線 y = 3 x を原点のまわりに 30° 回転した直線の方程式を求めなさい。<解説と解答> y = 3 x の x軸の正の向きとつくる角をαとすると、求める直線が x軸の正の向きとつくる角は α+30° となるから、その傾きは tan(α+30°)=(tanα+tan30°)/(1ーtanα・tan30°) = (3+√3/3) /(1ー3・√3/3) =ー(6+5√3)/3 よって、求める直線はy = ー[{(6+5√3/3)/3}/3]・ x …答えです。簡単ではありますが、大学入試の数学の問題です。tanの加法定理を使います。序理伊塾では算数や数学を分かり易く教えることに努めています。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
朝の散歩、親水公園です。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
2022年9月27日 先生と生徒(卒業生も)のふれあい広場






朝の散歩、親水公園です。最近は少し早めに7時30分に出発します。約一時間強の散歩。たくさんのワンちゃん達に出会います。毎日のように会うワンちゃん、時折会うワンちゃん、初めて会うワンちゃん、色々です。ワンちゃん達に会うのも朝の散歩の楽しみの一つとなっています。…ジョリーもきっとそうだと思います。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
大学入試の数学の問題です。算数個別、数学個別、序理伊塾。
2022年9月26日 先生と生徒(卒業生も)のふれあい広場
<問題> k は定数とする。直線 (k+3) xー(2kー1)yー8kー3=0 は、kの値に関係なく定点Aを通る。その定点 A の座標を求めなさい。<解説と解答> (k+3) xー(2kー1)yー8kー3=0…➀ とする。➀をについて整理すると k ( xー2yー8)+3 x+yー3=0 この等式が kの値に関係なく成り立つための条件は、 xー2yー8=0、3 x+y ー3=0 この連立方程式を解いて、 x=2、y = ー3 以上から求める定点Aの座標は (2、ー3)…答えです。大学入試の数学の問題です。「kの値に関係なく」は、「全てのkについて」、「任意のkに対して」、「kに対して常に」…などと表現されることもあります。いずれにしろ、大切な基本問題です。序理伊塾では算数や数学を分かり易く教えることに努めています。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
今日はジョリーのシャンプーの日です。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
2022年9月25日 先生と生徒(卒業生も)のふれあい広場






今日はジョリーのシャンプーの日です。場所は江東区猿江二丁目。歩いて40分程。結構あります。勿論、ジョリーはカート。でも、今日はいいことがありました。湿疹の具合がかなり良くなったので、二週間に一度が三週間に一度で、よくなったのです。マメに通った成果です。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
大学入試の数学の問題です。算数個別、数学個別、序理伊塾。
2022年9月24日 先生と生徒(卒業生も)のふれあい広場
<問題> 3点 A (6、13)、B(1、2)、C(9、10) を頂点とする△ABCにおいて、点Aを通り、△ABCの面積を2等分する直線の方程式を求めなさい。<解説と解答> 求める直線は、辺BCの中点を通ります。この中点をMとすると、その座標は x=(1+9)/2 = 5、y = (2+10)/2 = 6 で、(5、6) となります。よって、求める直線の方程式は 、yー13={(6ー13)/(5ー6)}×(x ー 6) より、y = 7x ー 29…答えです。簡単な問題です。求める直線の方程式は、辺BCの中点を通ります。この問題は中学数学としても出てきます。序理伊塾。では算数や数学を分かり易く教えることに努めています。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
我が家の愛亀の” はなちゃん “。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
2022年9月23日 先生と生徒(卒業生も)のふれあい広場



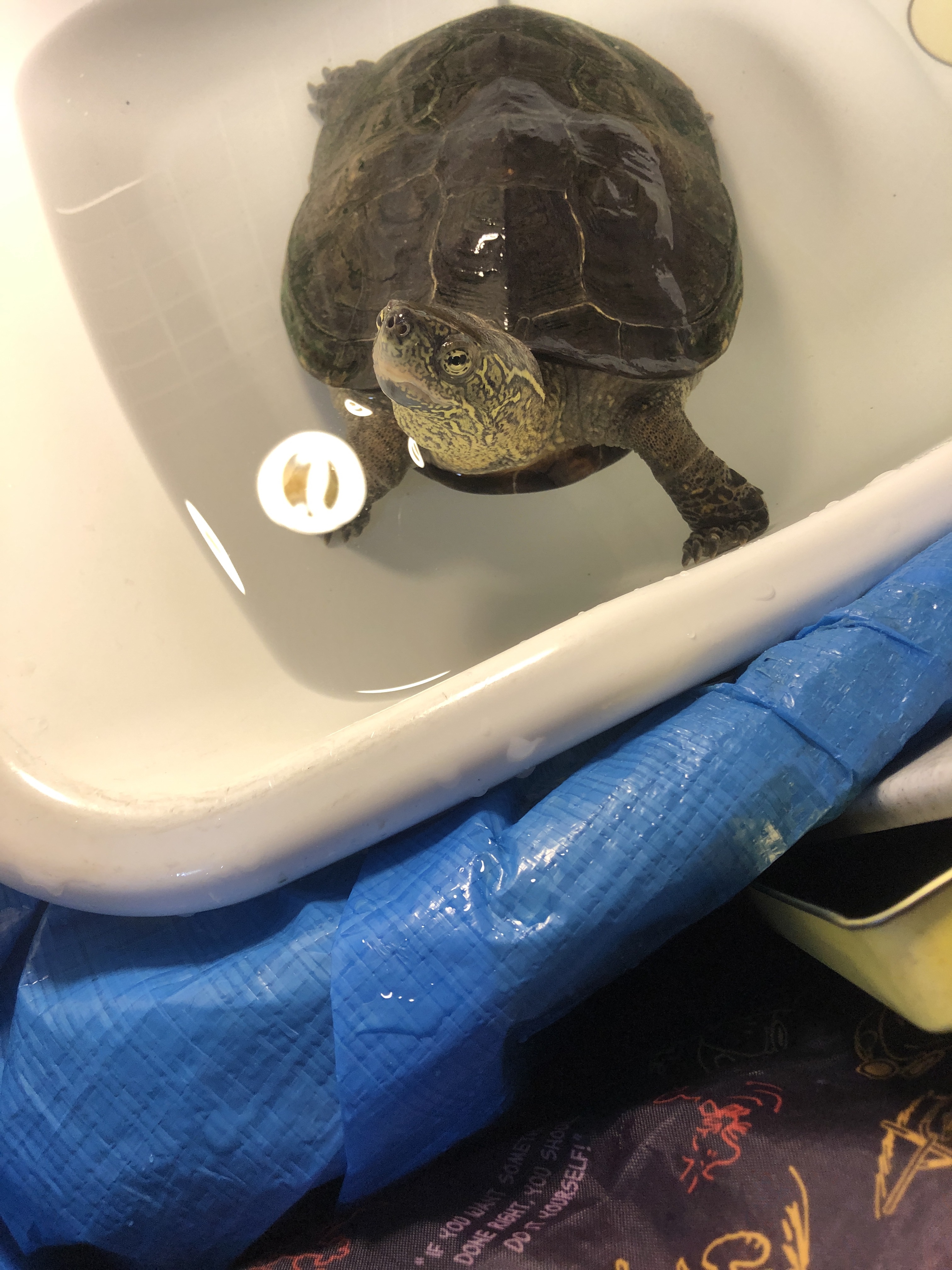
我が家の愛亀の” はなちゃん “。二代目のジョリーに保護されて我が家に来てから22年。年齢不詳です。少し前までは卵を一度に10個くらい産んでいたのですが、ここ2回は一つづつ。でも綺麗な卵です。年齢不詳の” はなちゃん “、我が家の家族の一員なのです。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
大学入試の数学の問題です。算数個別、数学個別、序理伊塾。
2022年9月22日 先生と生徒(卒業生も)のふれあい広場
<問題> 曲線 y = x x x+k x+2 が直線 y = 9 xー14 に接するように、定数 k の値を求めなさい。<解説と解答> y = x x x+k x+2 のとき、y′=3 x x+k x ここで、接点の x座標を αとすると 、y座標が一致することからααα+kα+2=9αー14…➀ 又、傾きが一致することから、3αα+kα=9…➁、➁から k=9αー14…➂ 、➂を➀に代入して ααα+(9ー3αα)α+2=9αー14 よって、ααα=8、αは実数なので、α=2 そして、➂から k=ー3…答えです。簡単ではありますが、大学入試の数学の問題です。接点の x座標を α とすることから始まります。後は、y座標と傾きが一致すればよいのです。序理伊塾では算数や数学を分かり易く教えることに努めています。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
序理伊塾からのお知らせです。【安心の完全後払い制】算数個別、数学個別、序理伊塾。
2022年9月21日 先生と生徒(卒業生も)のふれあい広場
<授業料変更のお知らせです>


20 :00〜22 :00 の時間帯の授業料を各学年ともに、それぞれの授業料の 一律30%引きに致しました。是非ご利用下さい。尚、序理伊塾へのお問い合わせでお急ぎの方は是非お電話を下さい。電話は、03ー3846ー6903 山岡です。【安心の完全後払い制】東京都 算数個別、数学個別、序理伊塾。

