問題…SHIKADAIという語の8文字全部を使って順列を作ります。3文字S、K、Dの位置はもとの位置と変わってもよいが、その順序だけは変わらないようにする場合は何通りありますか。解説と解答…SKDを同じ文字、例えばXで置き換えて、XHIXAXAIを一列に並べたものに対して3個のXのかわりに左から、S、K、Dと置き換えることによって、条件に適する順列が求まります。つまり、一つに一つが対応します。よって、8!÷(3!2!2!)=1680通りです。この問題は高校の数学で中学の数学の範囲ではありません。もちろん、中学入試の算数では必要ありません。大学入試の数学の基本です。算数でも数学でも柔らかな考え方が必要です。
月別アーカイブ: 2010年2月
懐かしい風景
2010年2月27日 先生と生徒(卒業生も)のふれあい広場
高校の数学の問題…その1
2010年2月26日 先生と生徒(卒業生も)のふれあい広場
問題…SHIKADAIという語の8文字全部を使って順列を作ります。左端が子音で右端が母音であるようにする場合は何通りありますか。解説と解答…左端に子音がくるのは4通り、右端に母音がくるのは2通り。間には異なる4個と同じものが2個の計6個の順列だから、6!÷2! だから、4×2×(6!÷2!)=2880通りです。この数学の問題はある大学の実際の入試の数学の問題です。算数では、無理のようです。個数がバラバラな文字の順列は高校の数学の公式にあります。是非、押さえておいて下さい。私の教室は個別指導なので、生徒がどの辺が解らないのか、把握することに努めています。
朝の散歩
2010年2月25日 先生と生徒(卒業生も)のふれあい広場
速さと比の基本問題…中学入試の算数
2010年2月24日 先生と生徒(卒業生も)のふれあい広場
問題…A君がB君と100メートル競争をしたら、10メートル負けました。では、B君の出発地点を何メートル後ろにすれば、2人一緒にゴールに着きますか。解説と解答…同じ時間に走る距離は比例します。A君とB君の同じ時間に走る距離の比は、(100−10):100で、問題はA君が100メートル走る間にB君が何メートル走ればよいかを出したいのだから、(100−10):100=100:□で □=111と1/9になります。111と1/9−100=11と1/9でこれが答えです。この問題は中学入試の算数の基本問題です。出来ないと困る算数です。大切なのは、同じ時間に走る距離は比例して、なおかつそれが速さの比になるということです。算数の速さの問題の基本です。この場合は誰が丁度100メートル走るかを押さえれば良いだけです。個別指導の私の教室では、初めてこの問題をやる生徒に、“丁度、100メートル走るのは誰?”と質問します。この算数の問題は必ず覚えて下さい。
銀座のお店
2010年2月23日 先生と生徒(卒業生も)のふれあい広場
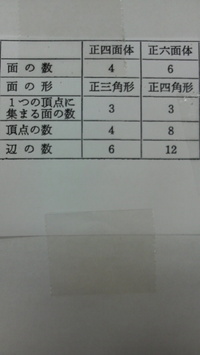
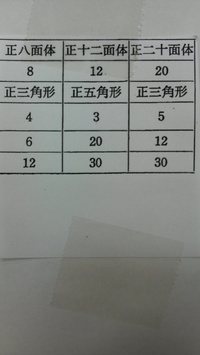
正多面体
2010年2月22日 先生と生徒(卒業生も)のふれあい広場
銀座のお店
2010年2月21日 先生と生徒(卒業生も)のふれあい広場
中学入試の算数の問題です。
2010年2月20日 先生と生徒(卒業生も)のふれあい広場
問題…40チームが参加して、野球の試合をトーナメント(勝ち抜き戦)で行います。引き分けはないものとして、優勝チームが決まるまでに全部で何試合行われますか。解説と解答…トーナメントでは、勝ち抜き戦なので1試合行うたびに1チームが敗退していきます。40チームのうち1チームが勝ち残るには40−1=39チームが敗退するので、39の負けがあります。ですから39試合あります。これは中学入試の算数です。中学の数学ではあまり見かけませんが、さっと解答を出せない生徒も多いのではないでしょうか。ここでは数学としてではなく、算数としておきます。
雪の朝の散歩
2010年2月19日 先生と生徒(卒業生も)のふれあい広場