月別アーカイブ: 2009年12月

今年は教室に新しい仲間が増えました。海水魚さん逹です。皆さん元気に泳ぎ回っています。ところで、算数と数学の個別指導塾、序理伊塾も開いてから約２０年が経ちました。昔の教え子から年賀状を含めて便りを貰いますが、とても嬉しいものです。算数や数学の力を付けて、入学試験に合格したりすることも、勿論嬉しいのですが、教え子が算数や数学を通して論理的な考え方を身に付けて、それぞれの好きな道で活躍して貰いたいと思っています。また、入学試験に関しては、「それぞれの志望校」を大切にしていきたいと思います。

問題…１から１００００の整数を全部書き並べるとき、数字の１を何回書くことになりますか。解説と解答…とりあえず、０から９９９９の１００００個の整数を考えます。そして、例えば１は０００１、１２は００１２というように０を補って４桁にして書くと、全部で４×１００００＝４００００個の数字を書くことになります。このとき０から９は均等に現れるので、４００００÷１０＝４０００回ずつ書くことになります。１だけは最後の１００００でさらに１回書くので、答えは４００１回です。この問題は一応、高校の数学としてとりあげられていましたが、中学の数学、さらには小学生の算数としても登場しそうです。又、この手法を使える類似問題が算数でも数学でも数多く見かけられます。個別指導の序理伊塾、お薦めの解法です。

５時３０分に起きて、オシッコをして体重を計って、食事が終わると先生は一息つけます。そして、勉強をしようとすると、ご覧の通り写真の左側です。パパ、なにするの？遊ぼうよ♪といったふうに覗き込みます。そして諦めて、No.５の上で大人しく私のことを見ています。写真の右側です。

問題…平面上に点Ａ(−２、７)と直線ｍ：２ｘ−３ｙ−１＝０があります。Ａから直線ｍに下ろした垂線の足Ｈの座標と直線ｍに関するＡの対称点、Ｂの座標を求めなさい。解説と解答…今回はベクトルで解いてみます。直線 ａｘ＋ｂｙ＋ｃ＝０に垂直なベクトルつまり法線ベクトルは(ａ、ｂ)であることを覚えていない人は必ず覚えて下さい。これがＡＨの方向ベクトルになるので、ＡＨの直線のベクトル方程式は(ｘ、ｙ)＝(−２、７)＋ｔ(２、−３)となります。ですから
ｘ＝２ｔ−２　ｙ＝−３ｔ＋７です。これを直線ｍに代入して　ｔ＝２
よってｔ＝２のときにＨとなり、その２倍のｔ＝４のときにＢとなります。ですから、Ｈ(２、１)　Ｂ(６、−５)　です。数学のこの種類の問題は数多く出てきますが、今回は数学でもベクトルでやってみました。ベクトルの苦手な人は是非マスターしてください。算数でも数学でも苦手な種類の問題を克服することが大切です。個別指導の私の教室では、苦手な問題を残して試験に臨んではいけないと常日頃から強調しています。

５時３０分に起きて、オシッコをして体重を計ったら次は、いよいよジョリーの楽しみな朝の食事です。ジョリーはまるで私をせかせるようにキッチンまで来て待っています。(写真左) ドッグフードを大さじ一杯、缶詰めを大さじ一杯でトッピング、ワンちゃん用の牛乳を大さじ４杯で出来上がり♪ 人間用の牛乳はいけないようです。そして、ジョリーの楽しみな朝の食事が始まります。食欲旺盛♪ あっという間に食べてしまいます。(写真右) 1日に３回の食事です。量は少ないようですが、獣医さんの指示通りにしています。お陰で、ウエイトコントロール、バッチリ！毛艶バッチリ！

問題…平面上に点Ａ(−２、７)と直線ｍ：２ｘ−３ｙ−１＝０があります。Ａからｍに下ろした垂線の足の座標とｍに関するＡの対称な点の座標を求めなさい。解説と解答…とりあえず、ｍと垂直な直線の式を出すのですが、ｍをｙ＝…に変えて、傾きどうしがかけて−１だから…は今回はやめて、次ののことを先ず覚えて下さい。ａｘ＋ｂｙ＋ｃ＝０に垂直な直線はｂｘ−ａｙ＋□＝０です。ここで、垂直の足Ｈは直線ｍとＡＨの交点になります。直線ＡＨはｍに直交するので、上記を利用して、３ｘ＋２ｙ＋□＝０と書けます。この直線は点Ａ(−２、７)を通るから代入して、□＝−８　よって、ＡＨは３ｘ＋２ｙ−８＝０、これと直線ｍの式を連立させて、ｘ＝２、ｙ＝１　垂線の足は(２、１)です。次にＡの対称点ＢはＡとＨを２：１に外分するので、外分の公式を使って、点Ｂは(６、−５)となります。内分と外分の公式は高校の数学では絶対に必要なもので、曖昧な人は完全に覚えて下さい。私の個別指導の教室では中学生の数学と
しても教えています。算数では出てこないと思います。この問題は高校の数学の教科書の応用例題としてもとりあげられていたような気がします。

毎朝５時３０分に私が起きると、ジョリーもたいていは起きてきて(一緒に寝ています)、まずはオシッコです。お尻を拭いてあげて、スイット、そして、ご褒美です。ジョリーはきちんとお座りをして待っています。つまり、きちんとオシッコシートの上にしたことを誉めて挙げるのです。次に、体重測定です。ジョリーは自発的に体重計の上に乗ります。この体重計はキログラムで小数第２位まで計れる優れものです。今日は７、４７キログラム、グッドです。次にジョリーのお食事になりますが、次回にします。

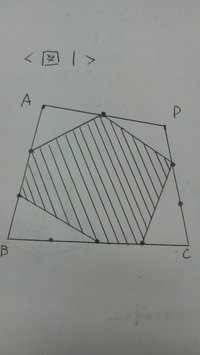
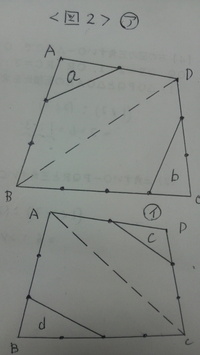
問題…図１に於て、斜線部分の面積は四角形ＡＢＣＤのどのくらいですか。解説と解答…図２のアに於て、ａ＝(１×１)÷(３×２)×三角形ＡＢＤ＝(１／６)三角形ＡＢＤ ｂ＝(１×２)÷(４×３)×三角形ＢＣＤ＝(１／６)×三角形ＢＣＤ よって、ａ＋ｂ＝(１／６)(三角形ＡＢＤ＋三角形ＢＣＤ＝(１／６)×四角形ＡＢＣＤ　又、イに於て、ｃ＝(１×１)÷(２×３)×三角形ＤＡＣ＝(１／６)×三角形ＤＡＣ ｄ＝(１×２)÷(３×４)×三角形ＡＢＣ＝(１／６)×三角形ＡＢＣ ｃ＋ｄ＝(１／６)(三角形ＤＡＣ＋三角形ＡＢＣ)＝(１／６)(四角形ＡＢＣＤ)　アとイから
ａ＋ｂ＋ｃ＋ｄ＝(１／６)(四角形ＡＢＣＤ)＋(１／６)(四角形ＡＢＣＤ)＝(２／６)(四角形ＡＢＣＤ)＝(１／３)(四角形ＡＢＣＤ)となります。ですから、斜線部分の面積はこれを引いて、四角形ＡＢＣＤの２／３です。この問題は中学の数学として最近生徒に教えたものですが、中学入試の算数としても登場しています。算数としても数学としても是非出来るようにしておいて下さい。算数でも数学でも、きちんと図を書く習慣が大切です。個別指導の私の教室では、算数においても数学においても、日頃から図をきちんと書くことを大切にしています。

一枚目の写真はペットショップのコジマさんの亀戸店です。亀戸天神の近所にあります。私は毎週、ここでジョリーのお土産を買います。二枚目の写真の馬〓のアキレスです。扱っているお店は結構少ないようです。とても固いので歯を綺麗に丈夫にしてくれます。私は教室の冷蔵庫に保管しておいて毎日、教室からの帰りに一本ずつジョリーにお土産としてもって帰ります。ジョリーはとても楽しみにしています。

問題…直径の両端がＡ(３、３)、Ｂ(５、−７)であるような円の方程式を求めなさい。解説と解答…ＡＢの中点、Ｏの座標を出してこれが円の中心で、ＯＡが半径になるから…では面倒なので、準公式を覚えておいて下さい。２点Ａ(ａ1、ａ2)、Ｂ(ｂ1、ｂ2)を直径とする円の方程式は(ｘ−ａ1)(ｘ−ｂ1)＋(ｙ−ａ2)(ｙ−ｂ2)＝０ なのです。だから、(ｘ−３)(ｘ−５)＋(ｙ−３)(ｙ＋７)＝０ で、これを整理して ｘｘ＋ｙｙ−８ｘ＋４ｙ−６＝０ となります。これの証明問題が大学入試の数学で出題されていたような気がしますが、その時は上記の方法でやれば良いのです。円はとても大切な数学の問題の一つです。数学の苦手な人もしっかりと覚えて下さい。勿論、算数でも、中学の数学のジャンルではありません。